Welcome to unit 6 study guide similar triangles, an immersive journey into the fascinating world of similar triangles. In this comprehensive guide, we will delve into the intricacies of these geometric shapes, uncovering their unique properties and exploring their diverse applications in various fields.
As we embark on this exploration, we will uncover the fundamental concepts of similar triangles, including their definitions and the remarkable properties that distinguish them from other triangles. We will then delve into the Triangle Proportionality Theorem, proving its validity and unlocking its power in solving a myriad of geometric problems.
Introduction: Unit 6 Study Guide Similar Triangles
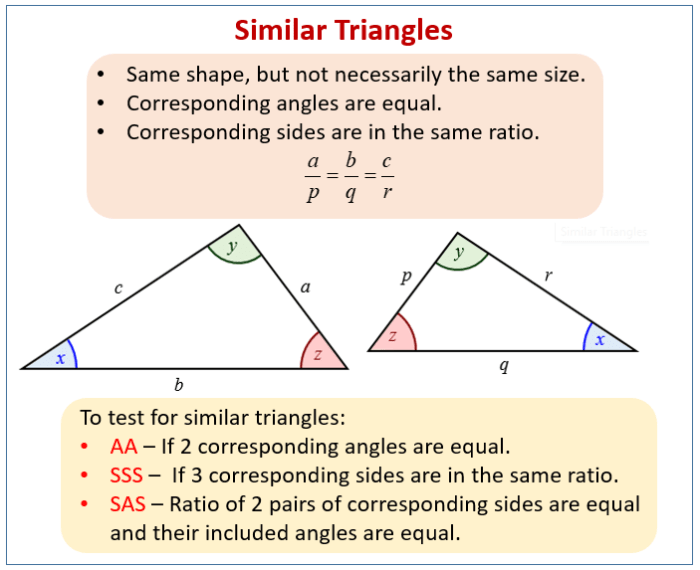
Similar triangles are triangles that have the same shape but not necessarily the same size. They are characterized by having their corresponding sides proportional to each other. This means that the ratio of any two corresponding sides is the same for all similar triangles.Similar
triangles have several important properties. First, their corresponding angles are congruent. This means that if two triangles are similar, then the corresponding angles will have the same measure. Second, the ratios of the lengths of their corresponding sides are equal.
This means that if two triangles are similar, then the ratio of the length of any two corresponding sides will be the same.Similar triangles are significant in real-world applications. They are used in architecture, engineering, and design to create structures that are both aesthetically pleasing and structurally sound.
For example, the pyramids of Giza in Egypt were built using similar triangles to ensure that the structures would be stable and symmetrical.
Theorems and Proofs

Triangle Proportionality Theorem
The Triangle Proportionality Theorem states that if a line parallel to one side of a triangle intersects the other two sides, it divides those sides proportionally. In other words, the ratio of the lengths of the segments created on one side is equal to the ratio of the lengths of the segments created on the other side.
To prove the Triangle Proportionality Theorem, let’s consider a triangle ABC with a line DE parallel to side BC. The line DE intersects side AB at point F and side AC at point G.
By the definition of parallel lines, we have the following proportions:
“`AF/FB = AG/GC“`
Multiplying both sides of this equation by FB, we get:
“`AF = (FB
AG)/GC
“`
Similarly, multiplying both sides of the equation by GC, we get:
“`FB = (GC
AF)/AG
“`
Therefore, the ratio of the lengths of the segments created on side AB (AF/FB) is equal to the ratio of the lengths of the segments created on side AC (AG/GC).
AA Similarity Theorem, Unit 6 study guide similar triangles
The AA Similarity Theorem states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
To prove the AA Similarity Theorem, let’s consider two triangles ABC and DEF with angles A and D, and angles B and E congruent, respectively.
By the Angle Addition Postulate, we have:
“`C = 180
- A
- B
F = 180
- D
- E
“`
Since A = D and B = E, we have C = F.
Therefore, the triangles ABC and DEF have three congruent angles, which means they are similar by the definition of similar triangles.
SAS Similarity Theorem
The SAS Similarity Theorem states that if two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar.
To demonstrate the SAS Similarity Theorem, let’s consider two triangles ABC and DEF with AB/DE = BC/EF and angle B = angle E.
By the Triangle Proportionality Theorem, we have:
“`AC/DF = BC/EF“`
Since BC/EF = AB/DE and angle B = angle E, we have:
“`AC/DF = AB/DE“`
Therefore, the triangles ABC and DEF have two pairs of proportional sides and a congruent included angle, which means they are similar by the definition of similar triangles.
Applications

Similar triangles find practical applications in various fields, including architecture, engineering, photography, and art.
One key application is using similar triangles to solve problems involving scale drawings. In architecture and engineering, blueprints and scaled models are often used to represent actual structures or designs. By understanding the relationships between similar triangles, architects and engineers can determine the actual dimensions of objects or structures based on their scaled representations.
Scale Drawings
- Problem:Determine the actual height of a building if its scale drawing is 1:200 and the height on the drawing is 5 cm.
- Solution:Let the actual height be h. We have the proportion h/5 = 200/1. Solving for h gives h = 5 – 200 = 1000 cm or 10 meters.
In photography and art, similar triangles are used to understand perspective and create realistic representations of three-dimensional objects on a two-dimensional surface. Artists and photographers use the principles of similar triangles to achieve depth and realism in their work.
Perspective in Art
- Concept:Objects farther away appear smaller and higher on the picture plane.
- Application:By understanding how similar triangles are formed as objects recede into the distance, artists can create the illusion of depth and distance in their paintings or drawings.
Examples and Exercises
This section provides examples and exercises to reinforce the concepts of similar triangles. It includes a comparison table, practice problems, and interactive exercises to enhance understanding.
Table of Similar and Non-Similar Triangles
The following table compares the characteristics of similar and non-similar triangles:
| Characteristic | Similar Triangles | Non-Similar Triangles |
|---|---|---|
| Side Ratios | Proportional | Not proportional |
| Angle Measures | Congruent | Not congruent |
| Area Ratios | Proportional to the square of the side ratios | Not proportional |
Practice Problems
Solve the following practice problems involving similar triangles:
- Triangle ABC is similar to triangle DEF. If AB = 6 cm, BC = 8 cm, and DE = 10 cm, find the length of EF.
- A right triangle has legs of length 3 cm and 4 cm. If a similar triangle has a leg of length 5 cm, find the length of the other leg.
- Two triangles have side lengths of 3:4:5 and 6:8:10. Determine if the triangles are similar.
Interactive Exercises
Design interactive exercises that reinforce the concepts of similar triangles, such as:
- Drag-and-drop activity to match similar triangles.
- Online simulation to explore the relationship between side ratios and area ratios.
- Quizzes or games to test understanding of similar triangle properties.
Advanced Topics
This section delves into advanced concepts related to similarity transformations, exploring their representation using matrices and their applications in computer graphics and animation.
Similarity Transformations
Similarity transformations are geometric transformations that preserve the shape of a figure while altering its size or orientation. They include translations, rotations, dilations, and combinations thereof.
Matrix Representation of Similarity Transformations
Matrices can be used to represent similarity transformations. A similarity transformation matrix is a 3×3 matrix that applies the transformation to a point in 2D space.
Applications in Computer Graphics and Animation
- Scaling:Similarity transformations are used to scale objects in computer graphics, making them larger or smaller.
- Rotation:They are also used to rotate objects, changing their orientation in space.
- Translation:Similarity transformations can translate objects, moving them from one location to another.
- Animation:Similarity transformations play a crucial role in animation, allowing objects to move and change shape over time.
Top FAQs
What are the key properties of similar triangles?
Similar triangles share the following properties: corresponding angles are congruent, and the ratios of corresponding side lengths are equal.
How can I prove the Triangle Proportionality Theorem?
The Triangle Proportionality Theorem can be proven using a series of similar triangles and the properties of proportions.
What are some real-world applications of similar triangles?
Similar triangles have numerous applications in fields such as architecture, engineering, photography, and art, where they are used to solve problems involving scale, proportion, and perspective.