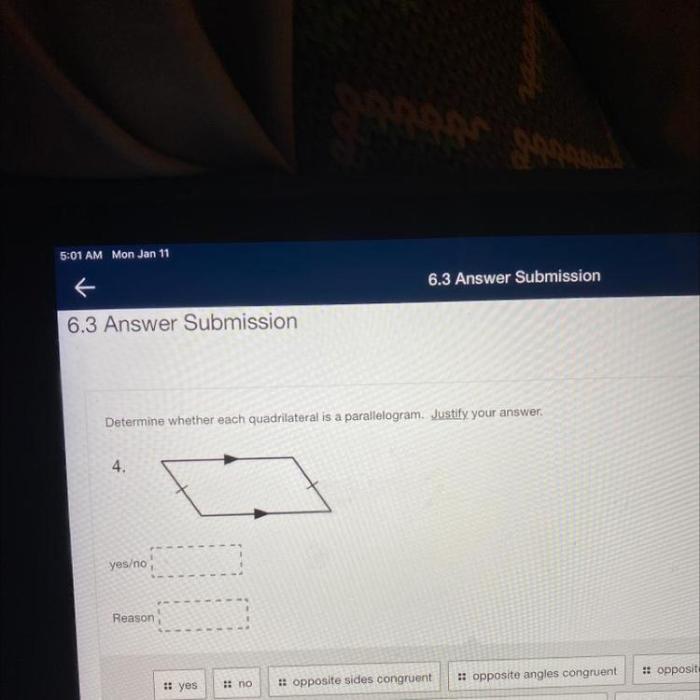
Determine whether each quadrilateral is a parallelogram. justify your answer – Determining whether a quadrilateral is a parallelogram is a fundamental task in geometry. This comprehensive guide provides a clear and concise definition of a parallelogram, Artikels its unique properties, and presents a step-by-step approach for identifying parallelograms. By understanding these concepts, you will gain a deeper understanding of quadrilaterals and their properties.

A parallelogram is a quadrilateral with opposite sides parallel and congruent. This distinctive characteristic sets parallelograms apart from other quadrilaterals and gives them their unique geometric properties.

Definition of a Parallelogram

A parallelogram is a quadrilateral that has two pairs of parallel sides.

Key characteristics that define a parallelogram include:

• Opposite sides are parallel and equal in length.
• Opposite angles are equal in measure.
• Consecutive angles are supplementary (add up to 180 degrees).
• Diagonals bisect each other.

Properties of a Parallelogram

Parallelograms have several unique properties that distinguish them from other quadrilaterals:

• Opposite sides are parallel and congruent.This property is a defining characteristic of parallelograms and is what sets them apart from other quadrilaterals.
• Opposite angles are congruent.This property is a consequence of the fact that opposite sides are parallel. When parallel lines are cut by a transversal, the alternate interior angles are congruent.
• Consecutive angles are supplementary.This property is also a consequence of the fact that opposite sides are parallel. When parallel lines are cut by a transversal, the consecutive interior angles are supplementary.
• Diagonals bisect each other.This property is unique to parallelograms and is not shared by any other quadrilateral.

Identifying Parallelograms: Determine Whether Each Quadrilateral Is A Parallelogram. Justify Your Answer

To determine whether a quadrilateral is a parallelogram, you can check for the following properties:

• Opposite sides are parallel and congruent.
• Opposite angles are congruent.
• Consecutive angles are supplementary.
• Diagonals bisect each other.

If a quadrilateral has all of these properties, then it is a parallelogram.

Justification of Parallelogram Identification

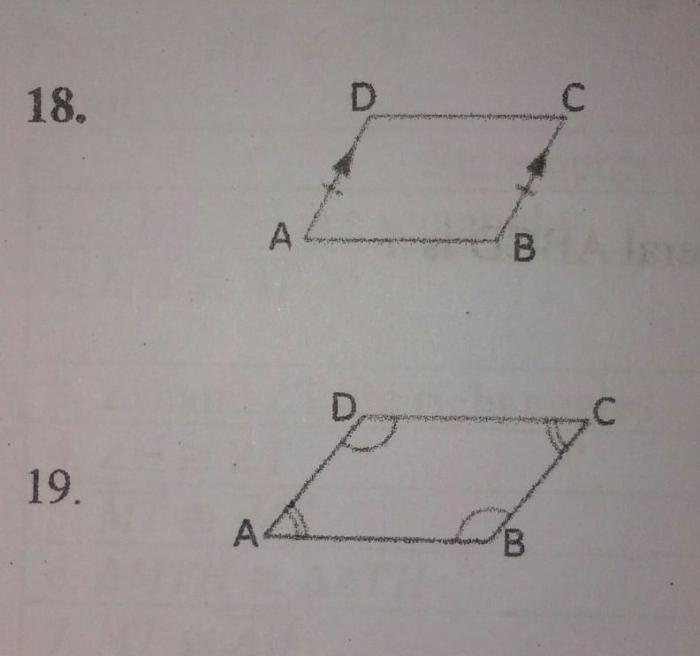
When you have determined that a quadrilateral has all of the properties of a parallelogram, you can justify your conclusion by stating the properties that you have checked and the reasons why the quadrilateral has those properties.

For example, you could say:

“I have determined that quadrilateral ABCD is a parallelogram because it has the following properties:

• Opposite sides AB and CD are parallel and congruent.
• Opposite angles A and C, and B and D, are congruent.
• Consecutive angles A and B, and C and D, are supplementary.
• Diagonals AC and BD bisect each other.

Therefore, quadrilateral ABCD is a parallelogram.”

FAQ Overview

What is the key characteristic of a parallelogram?

Opposite sides are parallel and congruent.

How can I determine if a quadrilateral is a parallelogram?

Check if opposite sides are parallel and congruent.

What are the unique properties of parallelograms?

Opposite sides are parallel and congruent, opposite angles are congruent, and diagonals bisect each other.